Automatisierte nichtlineare Parametervariation zur Schwingungsoptimierung reibungsbehafteter Strukturen

| Leitung: | Sebastian Tatzko |
| E-Mail: | foerster@ids.uni-hannover.de |
| Team: | Alwin Förster |
| Jahr: | 2023 |
| Förderung: | DFV und FVV |
| Laufzeit: | 01.01.2023-31.05.2025 |
Projektbeschreibung

Das Forschungsvorhaben fokussiert sich auf effiziente Berechnungsmethoden für stationäre Schwingungsantworten im Bereich der nichtlinearen Strukturdynamik, insbesondere in Turbomaschinen. Durch den Einsatz klassischer Modellordnungsreduktion und die Synthese von Frequenzgängen aus nichtlinearen Moden lassen sich Berechnungszeiten erheblich reduzieren.
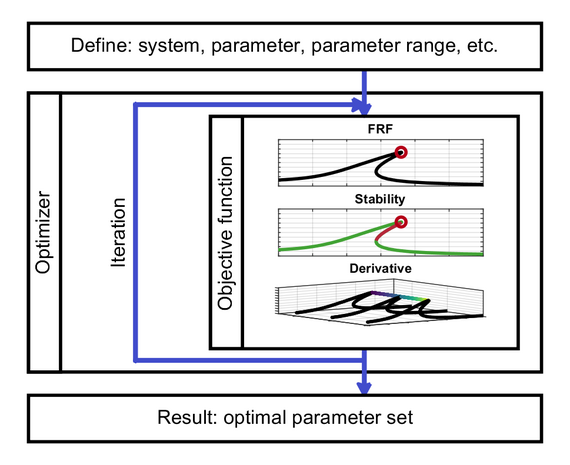
Das übergeordnete Ziel dieses Forschungsvorhabens ist die Entwicklung eines automatisierten Parameteroptimierungsprozesses, der speziell auf nichtlineare dynamische Probleme ausgerichtet ist. Hierbei sollen durch geeignet anzupassende Optimierungsmethoden die typischerweise verkoppelten Designparameter minimiert werden, um eine vordefinierte Kostenfunktion zu erfüllen. Die Grafik in Bild 1 veranschaulicht diesen Prozess übersichtlich.
Dieser innovative Ansatz zielt nicht nur darauf ab, aufwendige Parameterstudien, wie sie traditionell im Rahmen statistischer Versuchsplanung durchgeführt werden, zu vermeiden, sondern bietet auch eine automatisierte Lösung für die Diskretisierung von Parametersätzen sowie die Auswertung umfangreicher Datensätze. Der Fokus liegt dabei auf der Optimierung von zyklisch-symmetrischen Strukturen mit identischen Schaufel-Scheibe-Segmenten in Turbomaschinen, wobei lokale nichtlineare Kräfte in Reibkontakten wirken.
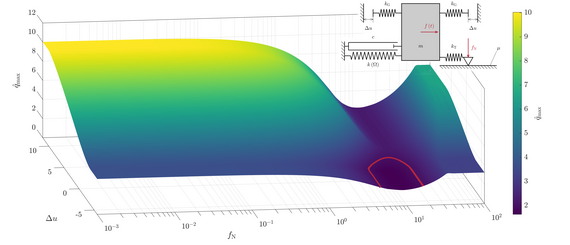
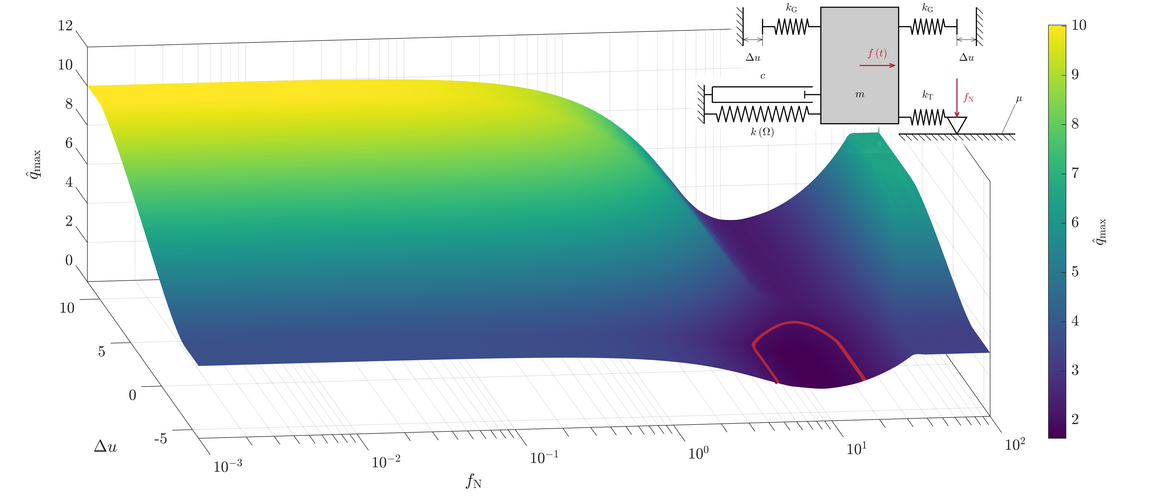
Zahlreiche Fragen müssen beantwortet werden, um diese Ziele zu erreichen. Hierzu gehören die Bewältigung numerischer Herausforderungen wie Konvergenzprobleme bei etablierten Berechnungsverfahren für nichtlineare Schwingungsantworten sowie die Auswahl optimaler Optimierungsverfahren für nichtlineare Strukturschwingungen. Besondere Aufmerksamkeit gilt auch den Auswirkungen sprunghaft veränderlicher Amplitudenantworten auf die Optimierung und der Möglichkeit einer adaptiven Optimierung je nach dynamischer Komplexität der Schwingungsantwort. Diese Fragestellungen werden sowohl aus der Perspektive der Grundlagenforschung als auch im Hinblick auf die industrielle Anwendbarkeit betrachtet. Die akademische Forschungsarbeit bildet die Grundlage für den späteren Transfer auf reale Anwendungsfälle und dient als Referenz für die entwickelten Verfahren. Es werden niedrigdimensionalen Referenzmodelle (Bild 2) untersucht, um den Wissensstand in der Forschung zur Optimierung nichtlinearer Schwingungsprobleme zu erweitern. Schließlich werden die entwickelten Verfahren an einem anwendungsnahen Beispiel in enger Zusammenarbeit mit der Industrie auf ihre Effektivität geprüft.


