Multiresonanzen und Multigrenzzykel
| Leitung: | Dr.-Ing. Lars Panning-von-Scheidt |
| E-Mail: | niklas.marhenke@ids.uni-hannover.de |
| Team: | M. Sc. Niklas Marhenke (Dynamik rotierender Maschinen) |
| Jahr: | 2019 |
| Förderung: | Industrie |
Bei der Auslegung von Turbinenschaufeln sind nichtlineare Koppelelemente zur Erhöhung von Steifigkeit und Dämpfung oft unumgänglich. Infolgedessen gelten lineare Gesetze nicht mehr, sodass ein Energietransport zwischen den Schwingungen einzelner Knotendurchmessern vorliegen kann. Mithilfe eines Minimalmodells mit wenigen Freiheitsgraden werden in diesem Projekt die Phänomene inspiziert, welche zwei in der Nähe eines kommensurablen Verhaltnisses stehenden Eigenfrequenzen nach sich ziehen. Dabei lassen sich drei Varianten der Kommensurabilität unterscheiden: 1:1- Resonanzen weisen nahezu identische Eigenfrequenzen auf, 1:n-Resonanzen entstehen durch ein ganzzahliges Verhältnis zweier Eigenfrequenzen und als dritte Möglichkeit besitzen die zu untersuchenden Eigenfrequenzen bei einer n:m-Resonanz näherungsweise einen gemeinsamen Teiler, ohne Vielfache voneinander abzubilden.
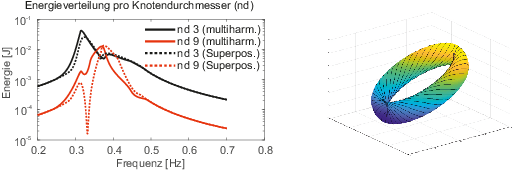
Auf der Basis von nichtlinearen Lösungsverfahren wird der eingeschwungene Zustand unter Beachtung der zyklischen Randbedingungen erforscht. Dabei gilt es, den Effekt auf den Energiefluss zwischen den Moden abzubilden. Als Einflussfaktoren für die Höhe des Energieflusses gelten beispielsweise die Phase, der Dämpfungsgrad und die Anregungskraft. Auch die Fragestellung, ob es Unterschiede beim Energiefluss innerhalb einer oder zwischen zwei verschiedenen Schwingungsfamilien gibt, wird untersucht. Zudem gilt es, die Besonderheiten der multiharmonischen Anregung im Vergleich zu einer Superposition zweier einzeln gerechneten Anregungsfälle aufzuzeigen. Hierbei liegt ein Augenmerk auf der Frage, welche weiteren Moden durch interne Resonanzen angeregt werden.
Neben den fremderregten Schwingungen weisen auch selbsterregte Schwingungen Energietransport zwischen verschiedenen Knotendurchmessern auf. Auf diese Weise treten quasiperiodische Lösungen auf, sobald die Eigenfrequenzen nicht exakt kommensurabel sind. Dadurch sind Erweiterungen der genannten Verfahren notwendig, um die Lösung berechnen zu können. Hierbei wird festgestellt, unter welchen Bedingungen welche Knotendurchmesser an der Lösung beteiligt sind. Außerdem ist die Abhängigkeit der Lösung von den Anfangszuständen Teil der Untersuchungen.


